Cómo ganar un concurso de televisión gracias a las matemáticas

El titular es un poco pretencioso, ya que primero tendrías que encontrar un concurso que se realice según la mecánica concreta que se expone a continuación.

Seguro que alguna vez has visto algún concurso donde al participante se le presentan varias puertas y detrás de una de ellas se encuentra el premio. Lo normal en estos casos es que una vez que se haya elegido una, el presentador vaya abriendo las puertas no elegidas hasta quedarse con dos (la elegida por el concursante y otra), de forma que se le añade una tensión extra que mantiene en vilo a los espectadores. Para añadir más emoción es probable que el presentador ofrezca al participante la posibilidad de cambiarse a la otra puerta que no ha sido desvelada o que se mantenga en su decisión inicial. Ya has visto concursos de este tipo alguna vez, estoy seguro. Pues bien, vamos a ver cómo las matemáticas (más concretamente la estadística) nos permite aumentar las posibilidades de llevarnos el premio.

¡Empieza el concurso! Eres el participante y te muestro tres puertas idénticas (A, B, y C) tras las cuales hay un coche y dos cabras. Es evidente que te quieres llevar el coche y que a priori puede estar en cualquiera de las tres puertas, así que supongamos que eliges la puerta A por pura intuición. Ahora abro una de las puertas que no elegiste, la B, y muestro una cabra. Perfecto, ahora sabemos sin lugar a dudas que tras una puerta se encuentra el coche y tas la otra la cabra que falta. Te ofrezco la posibilidad de quedarte en la A o cambiarte a la C, ¿qué harías?

Piénsalo bien.

Si has decidido mantenerte en la A seguramente habrás pensado que al quedar sólo dos puertas tienes 50% de probabilidad de llevarte el coche elijas la puerta que elijas. Pero te has equivocado.

Antes de explicarlo intentaré que lo entiendas por ti mismo. Para ello imagina que volvemos a realizar el concurso con la diferencia de que ahora son 100 puertas (con un coche y 99 cabras). Eliges una aleatoriamente y yo voy abriendo las demás puertas que son cabra hasta que nos quedamos con la puerta que has elegido y otra. ¿De verdad no te cambiarías? ¿Sigues pensando que hay 50% de probabilidades de ganar el coche en cualquiera de las 2 puertas? La realidad es que si te quedas tienes un 1% de posibilidades de ganar, pero si te cambias tienes el 99%. ¡Sería ilógico no cambiarse! De hecho, aunque hubiese abierto todas las puertas menos 5 (en vez de abrir todas menos una), hubieses tenido más posibilidades de ganar cambiándote a cualquiera de esas 3 puertas: tendrías 19,8% de probabilidades de ganar eligiendo cualquiera de esas 3 puertas, pero tendrías un mísero 1% si te quedases en la inicial.

¿Todavía no lo tienes claro? Volvamos al ejemplo original (el de las 3 puertas). Esta tabla muestra las 3 posibilidades que hay en un inicio y en cuáles de esas situaciones ganaríamos quedándonos o cambiándonos (partiendo de que elegimos inicialmente la puerta A):

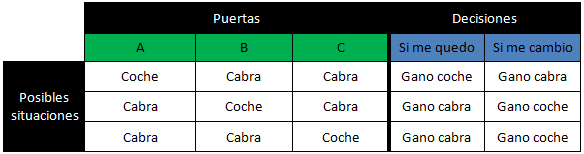
Si nos fijamos, vemos que si nos quedamos tenemos una posibilidad entre 3 de ganar el coche, pero si nos cambiamos tenemos 2 posibilidades entre 3, por lo tanto siempre conviene cambiarse.

Este planteamiento surgió precisamente a partir de un concurso televisivo que seguía esta mecánica de juego y hoy en día es conocido como el problema de Monty Hall, en honor al presentador del programa.